Answer to What is Penrose Triangle in short is, It is an art but impossible to exists! It is impossible for the Impossible Triangle to exist because in order for it to exist rules of Euclidean geometry would have to be violated.
What is Penrose Triangle?
The tribar/triangle appears to be a solid object, made of three straight beams of square cross-section which meet pairwise at right angles at the vertices of the triangle they form. The beams may be broken, forming cubes or cuboids.
Nerd Alert
This combination of properties cannot be realized by any three-dimensional object in ordinary Euclidean space. Such an object can exist in certain Euclidean 3-manifolds, and can also exist in 5-dimensional Euclidean space, which is the lowest-dimensional Euclidean space within which the Penrose triangle can be embedded.
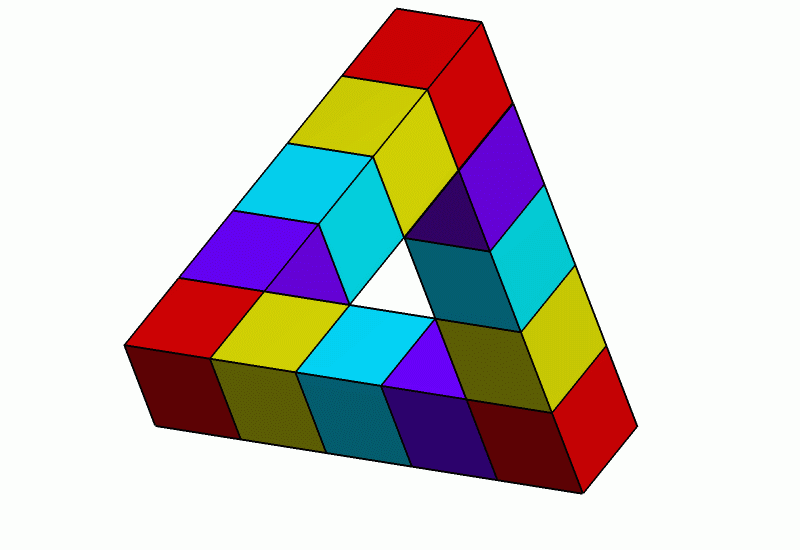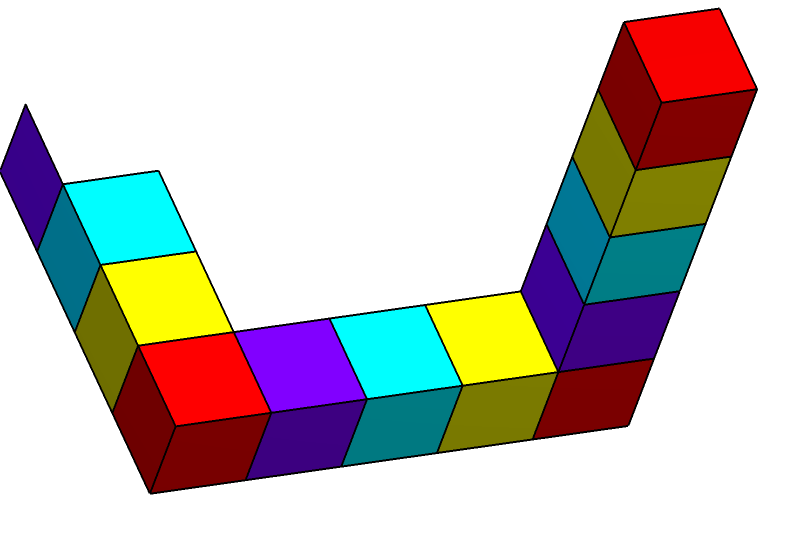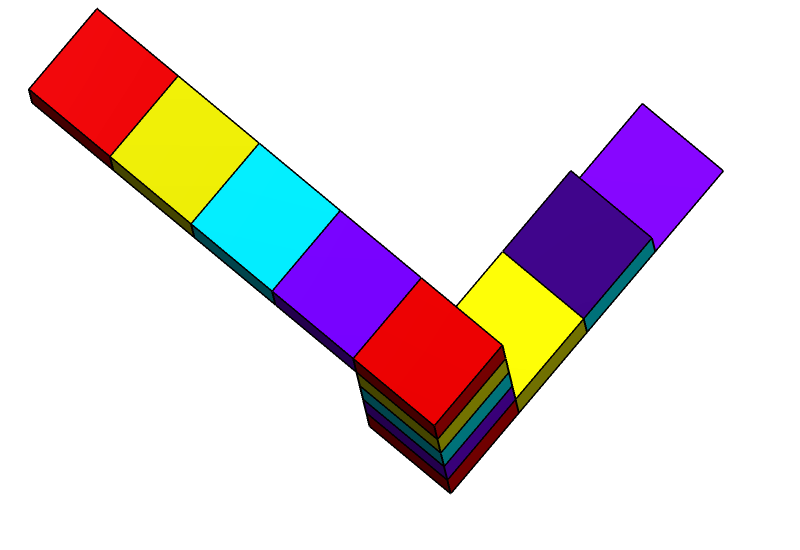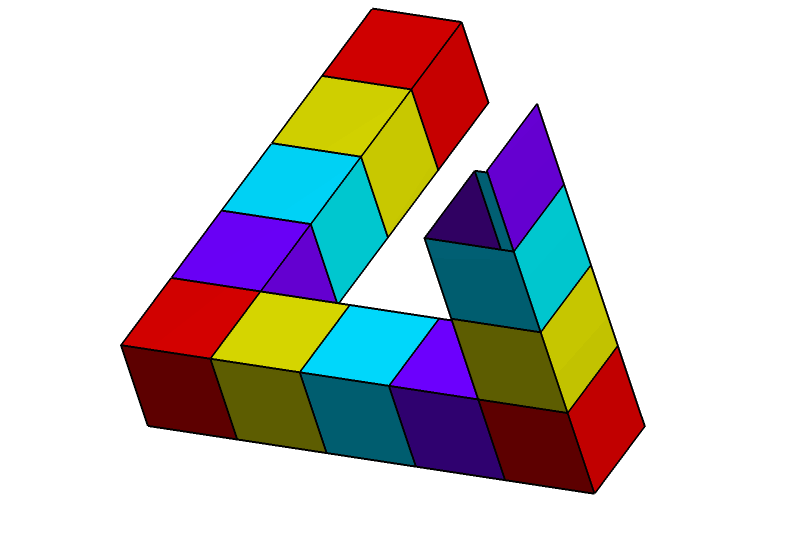
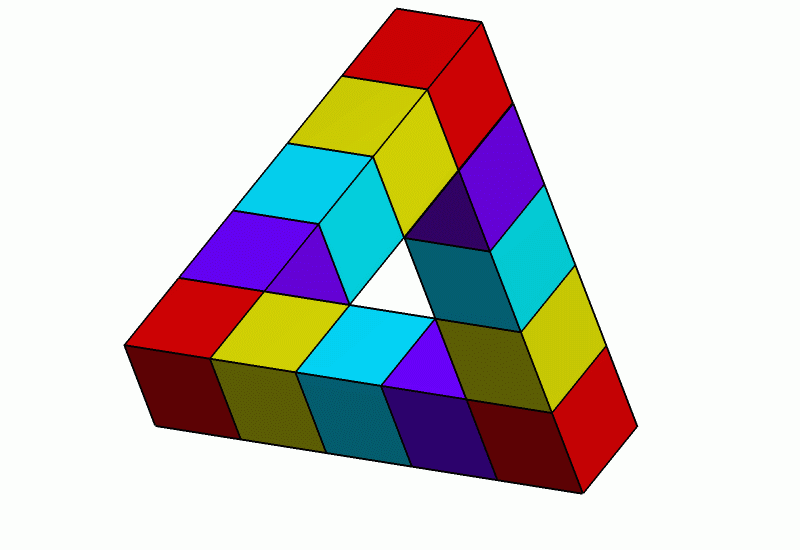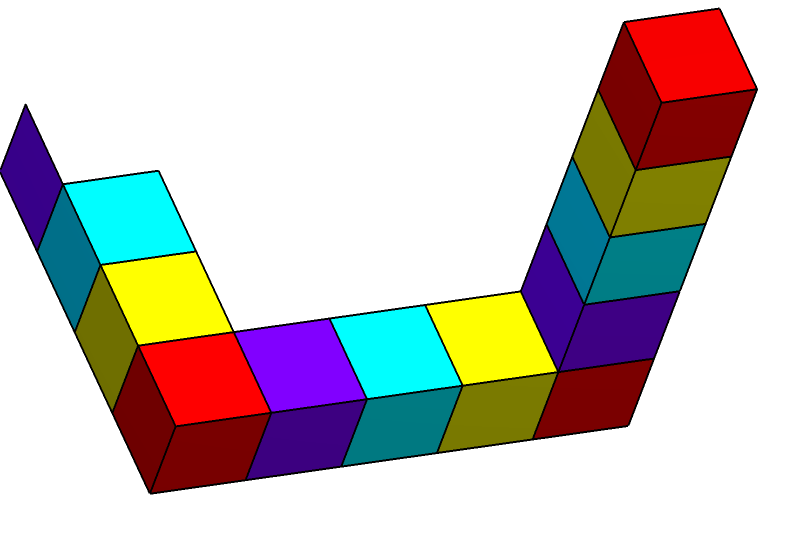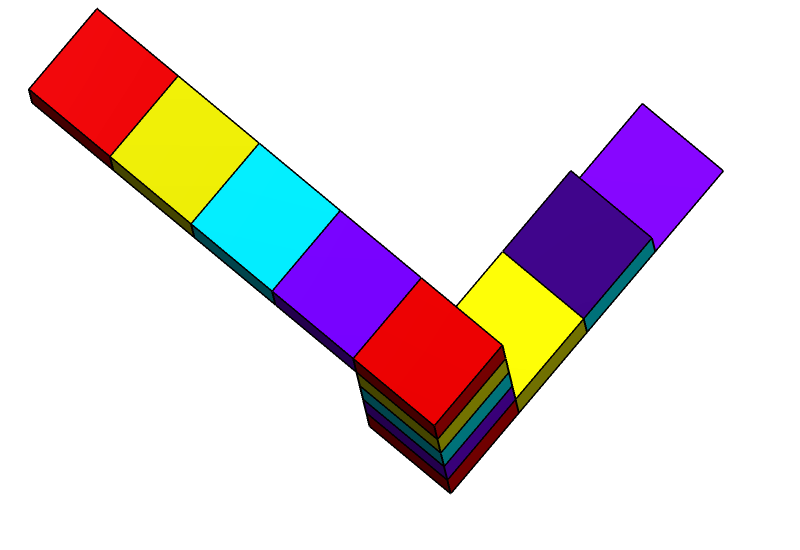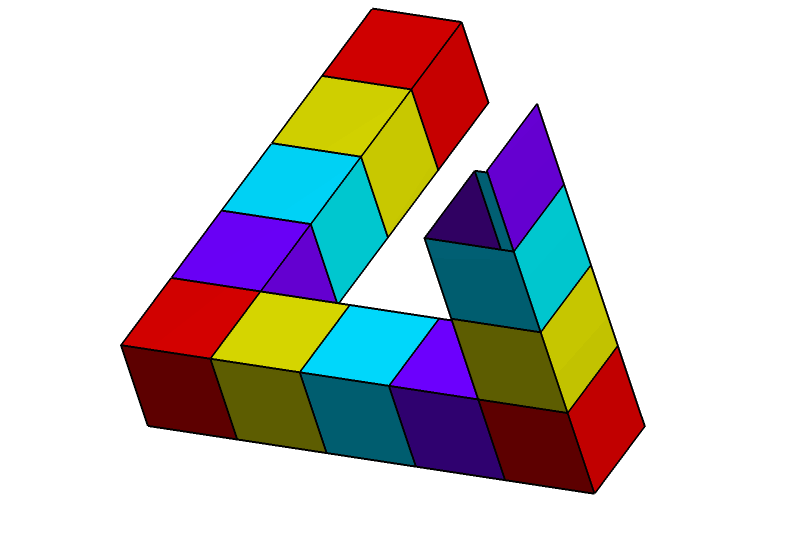
Penrose Triangle Sculpture! – Purchase It 🛍️


Well, It’s not possible with straight lines but sky’s the limit!
-
3D LED Moon and Galaxy Lamp – Touch Control – Perfect Craftsmanship
$19.99 -
Arc Reactor Building Blocks Set – Arc Reactor with LED Light – Iron Man Arc Reactor
$26.99 -
Arc Reactor Desk Toy – Arc Reactor Building Block – Restore Classic Movies Building
$29.99 -
Astronaut Building Block Compatible with Lego Space Model – Spacesuit with LED Light – Cool Collectible
$29.99 -
Astronaut Spacesuit Building Sets – Flexible Astronaut Space Toy with High Details
$53.94 -
Balrog Building Block Set – Balrog of Moria Building Block Set – Lord Of The Ring Balrog Desk Toy
$18.99 -
Crystal Snow Globe With Sand Clock – Eiffel Tower – Astronaut – Home Decoration – Desktop Decor Table Centerpieces Ornaments
$24.99 -
Dancing Ferrofluid Music Mate – Dancing Ferrofluid With Music Rhythm – Magnet Liquid Toy – Cool Gadget
$129.00 -
Disney Virtual Pet – Japanese Virtual Pet With Disney Characters – Mickey Mouse, Minnie Mouse, Nemo, Frozen, Moana, The Lion King, Beauty and the Beast
$34.99
It was first created by the Swedish artist Oscar Reutersvärd in 1934. Independently from Reutersvärd, the triangle was devised and popularized in the 1950s by psychiatrist Lionel Penrose and his son, the mathematician and Nobel Prize laureate Roger Penrose, who described it as “impossibility in its purest form”.



















